Изготовление уникальных металлических значков на заказ - это прекрасный способ добавить индивидуальность и стиль
Похмелье — это состояние, которое многие из нас испытывали после употребления алкоголя. Чувство недомогания,
Лампа-лупа является незаменимым помощником у целого ряда специалистов, например: косметологов, парикмахеров, массажистов и, конечно,
Накрутка жалоб в социальной сети ВКонтакте является одним из инструментов управления онлайн-репутацией и защиты
Переподготовка по психологии позволяет специалистам оставаться в курсе последних научных исследований, теорий и практических
В мире строительства каждый мастер понимает, что правильный выбор инструментов – залог успешного и
Флорариумы - это красивые миниатюрные сады, созданные в стеклянных контейнерах, где растения и элементы
При выборе квартиры в агентстве недвижимости, необходимо учитывать множество факторов, которые могут повлиять на
При необходимости пробить номер телефона часто прибегают к услугам профессионалов, таких как детективное агентство
Получить и использовать промокод Ашан достаточно просто. Необходимо выбрать подходящий промокод, ввести его в
Выбирая сумку на лето, подумайте о ее универсальности. Идеальная сумка должна хорошо сочетаться как
Лето – это пора свежести и ярких впечатлений. Важным элементом летнего образа является обувь.
Психологическая консультация – это важный инструмент, который помогает людям справляться с различными эмоциональными, психологическими
В современном мире смартфон является не просто устройством связи, а многофункциональным инструментом, который помогает
Мебель играет ключевую роль в создании атмосферы и комфорта в каждом доме. Она не
Свадьба – одно из самых ярких и значимых событий в жизни каждого человека. Этот
Особенно привлекательным направлением является Белек – райский уголок на юге страны, известный своими роскошными
Зимние букеты — это не только прекрасный способ добавить уюта и тепла в холодные
Пятигорск, расположенный в живописных предгорьях Кавказа, не только известен своими лечебными источниками, но и
Аренда зала фотостудии — важный шаг для профессиональных и любительских фотографов, стремящихся создать высококачественные
Реставрация изделий – это не просто процесс восстановления материальных ценностей, но и уважение к
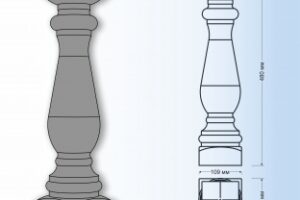
Создание деревянных балясин для лестницы собственными руками – это захватывающее и творческое предприятие, позволяющее
В эпоху цифровых технологий и онлайн-шопинга промокоды стали неотъемлемой частью розничной торговли и маркетинга.
Обращение в специализированный салон штор в Москве позволит получить профессиональную консультацию и помощь в
Покупка обуви в интернете становится всё более популярной из-за своей удобности и широкого ассортимента.
ЕГЭ (Единый государственный экзамен) – это важный этап в жизни каждого выпускника средней школы.
Сервис доставки "Макароллыч" – это отличное решение для тех, кто хочет наслаждаться вкусными суши
Рекламная акция с использованием купонов и промокодов может стать отличным способом привлечь новых клиентов